Re: In other news today...
-
@Tsaukpaetra said in In other news today...:
@anotherusername said in In other news today...:
the general formula for volume of an isosceles triangle in polar coordinates.
WTF is that even? You memorized that but you didn't memorize the formula for the volume of a cone?
@tsaukpaetra actually, the formula for any triangle. One half bee ache.
Uh... I mean, ½bh.
Coincidentally, it's exactly half of the area of a rectangle, which even you probably remember (as it's just the simple product of its two sides).
And for good reason it is. Take any triangle and set it upon one side to form a base, such that the two angles where the sides meet the base are both acute (as there can only be at most one obtuse or right angle, that angle would simply have to form the peak):
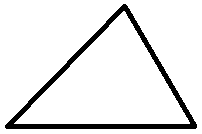
Dissect it by means of a vertical line that passes through its peak and at right angles to the base:
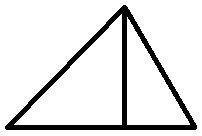
Take one of the two right triangles thus formed, and move it over to the other side:
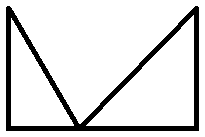
Note that, to this point, we have not changed the area of the shape -- merely sliced it and moved the pieces around.
Also note that the negative space between the two triangles looks rather suspiciously like the original triangle -- and if we take the original triangle and rotate it 180°, this suspicion is confirmed. It's an exact fit:
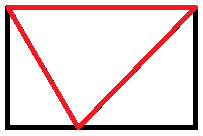
Now we have a rectangle, and we created it by adding the area of the original triangle once again: we've doubled its area. Its area is now quite easy: the length of its base (the same base as the triangle had) times the height (the length of the line that we used to slice it into two). Therefore, the area of the triangle is half of the size of the square: ½bh.
-
@anotherusername I think the issue was the in polar coordinates piece.
And the volume of a cone is easy:
1/3(area)*(height) = 1/3 pi r^2 h
-
@benjamin-hall I actually can't remember quite what I did anymore. I did end up with ⅓πr2h, though.
I remember checking that I was doing the integration properly by making sure that when I did the integration for a cylinder, I ended up with πr2h (since that one's easy to remember), before I did the same integration for the cone instead.
-
I think I remember... I integrated the area of a circle vertically to get the volume. The radius of the circle progresses in a linear fashion from r at the base to 0 at height h.
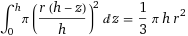
I had originally meant to use polar coordinates until I realized that this was much simpler since I already knew that the area of a circle is πr2 and that the radius at height z was easily calculated by multiplying r by the ratio of h - z to h. (Or just by the ratio of z to h, which effectively turns the cone upside down but produces the same exact result.)
-
I guess score negative points for learning by repetition then, since I eventually took calculus three times by the time I finished college and don't remember any of the above, except the area of a triangle. Because that one's one step away from area of a square, and even then it took up less than seven seconds to validate that from long-term storage....
-
THE SUM OF THE SQUARE ROOTS OF ANY TWO SIDES OF AN ISOSCELES TRIANGLE IS EQUAL TO THE SQUARE ROOT OF THE REMAINING SIDE
-
@anonymous234 THAT'S A RIGHT ANGLE TRIANGLE, IDIOT
-
@anonymous234 said in Re: In other news today...:
THE SUM OF THE SQUARE ROOTS OF ANY TWO SIDES OF AN ISOSCELES TRIANGLE IS EQUAL TO THE SQUARE ROOT OF THE REMAINING SIDE
You heartless straw man!
-
For those who missed the reference (psst, @bb36e)
-
@anotherusername said in Re: In other news today...:
For those who missed the reference (psst, @bb36e)
I never watched oz...
-
@scarlet_manuka said in In other news today...:
usual integration
For those of us who naturally reach for calculus when solving problems...

-
@tsaukpaetra I'd be interested to see your solution to the problem of "find the formula for the volume of a cone with a base of arbitrary shape and known area and a given height" that doesn't use calculus.
Incidentally, the usual integration for the volume of a cone is along the lines of @anotherusername's post above, except that we use the fact that the area of each cross-section scales quadratically. For convenience, set it up with x=0 being the apex and x=h being the base, then the area at a given point x is A (x/h)² where A is the base area. Integrating this for x on [0, h] very easily gives a volume of 1/3 Ah.
-
@tsaukpaetra There are some problems where it makes sense to reach for calculus. However, for most of us, those problems are few and far between. It's been quite a long time since I reached for calculus, and I'd have to reach back 30+ years to remember any of it if I did need to reach for it.
-
@hardwaregeek I've used it a couple of times in my current work. Things like repayment calculations for loans, which (when the repayment period is not the same as the interest period) don't have a nice solution and are typically found iteratively - I was able to give the guys implementing the calculator an equation derived from applying the Newton-Rhaphson method to the problem that they could run a few times to get a sufficiently accurate answer.
-
I have known how to integrate in polar coordinates, but I couldn't tell you offhand how to do it anymore. But now that it's been brought up I will probably end up checking wikipedia for it some time today.
-
@pleegwat all I really remember is that you should be able to integrate r (as a constant, I think) and produce πr2.
-
@scarlet_manuka said in Re: In other news today...:
@tsaukpaetra I'd be interested to see your solution to the problem of "find the formula for the volume of a cone with a base of arbitrary shape and known area and a given height" that doesn't use calculus.
In my current degraded state I probably would not be able to do so. With or without calculus.
-
@pleegwat said in Re: In other news today...:
I have known how to integrate in polar coordinates, but I couldn't tell you offhand how to do it anymore. But now that it's been brought up I will probably end up checking wikipedia for it some time today.
Generically, to change coordinates for integration, the main thing is calculating the volume element. Express each of the old coordinates in terms of the new, form the matrix of first partial derivatives, and take the absolute value of its determinant - this gives you the new volume* element.
In this case we'd look at cylindrical polar coordinates (r, θ, z) with the translation to (x, y, z) given by x = r cos θ, y = r sin θ (and z = z, obviously).
∂x/∂r = cos θ, ∂y/∂r = sin θ, ∂z/∂r = 0
∂x/∂θ = -r sin θ, ∂y/∂θ = r cos θ, ∂z/∂θ = 0
∂x/∂z = 0, ∂y/∂z = 0, ∂z/∂z = 1
Putting this into a matrix and taking the determinant gives r cos² θ + 0 + 0 - 0 + r sin² θ - 0 = r. So the new volume element is r dr dθ dz.(Obviously, in normal use this and other well-known coordinate transformations would not be recalculated each time.)
For a right circular cone we have the region z in [0, h], θ in [0, 2π], and r in [0, Rz/h] where R is the base radius. So we get
∫(0 to h) ∫(0 to 2π) ∫(0 to Rz/h) r dr dθ dz
= (2π) ∫(0 to h) [r² / 2][0 to Rz/h] dz
= π (R/h)² [z³ / 3][0 to h]
= (π/3) R²h.* Not specific to three dimensions, but naming things is hard, especially in arbitrary numbers of dimensions.