Labeling a pie chart
-
I've been doing a lot of HTML5 canvas work lately, and coincidentally I'm taking Plane Trigonometry which has been helpful to me in my current task.
The problem: I have to dynamically graph out a pie chart. Each pie slice has a color (hue, in HSL), a percentage, and a label. The pie chart renders fine, the problem is that I need to render a text label for each pie slice.
I'm using the unit circle from my trig class to dynamically find aesthetic positions for text labels surrounding the chart. I'm calling these points "anchors". Each pie slice needs to have a line from the pie slice to the label anchor point. The problem is selecting the best text anchor point for each slice.
The naive solution: As a first stab at the problem, I took each anchor point and used the Pythagorean theorem to calculate the distance to each pie slice [spoiler](actually the square root step is superfluous because if |x| > |y|, then sqrt(x) > sqrt(y))[/spoiler]. I then pick the shortest line and map that slice to an anchor, remove slice and anchor from the set needing mapping, and repeat until all points are mapped.
It works great!
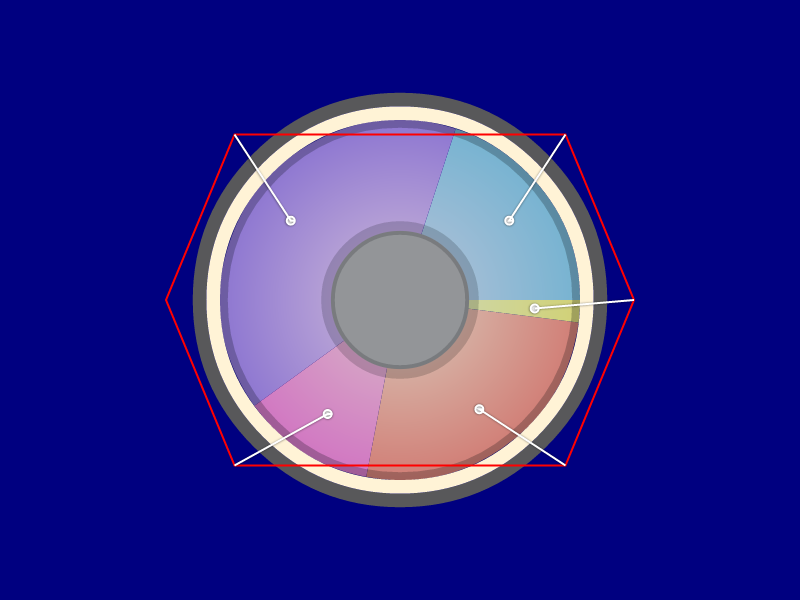
Except when it doesn't...
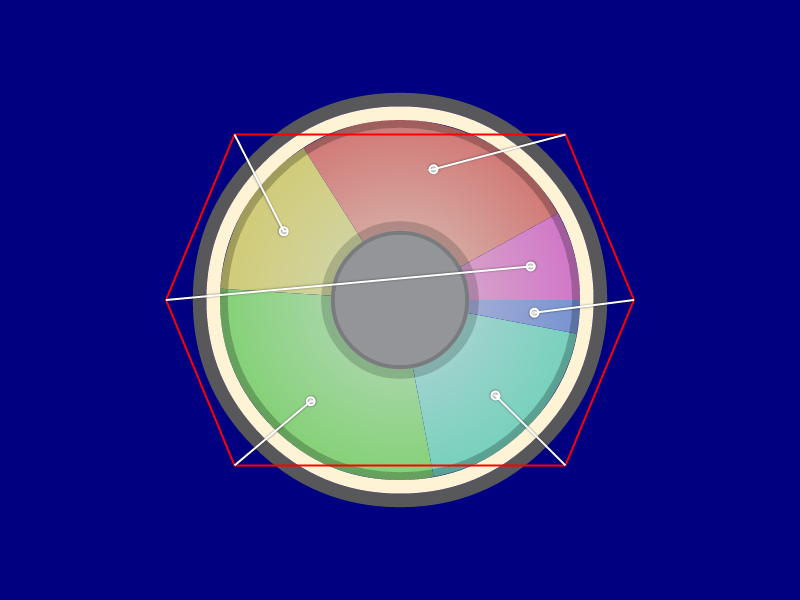
So, what happened here is slice 1 (they go counterclockwise from (1,0)) wasn't the closest to any anchor point, so it got mapped last and was stuck with whatever anchor was left over.
The solution: It seems like the best thing to do is to look at the sum of all lengths for all possible mappings and select the combination with the smallest total line length. Except that seems like it would be O(n!) (factorial) time.
Is there a more efficient way to accomplish this?
Edit: If rotating the pie chart could make the slices line up to anchors better, I would love to do that, but I really have no idea how to determine programatically whether rotation would be helpful, let alone how much.
-
I'm not sure that your method beats just taking straight lines out from the circle's center, but that also would have problems with narrow slices.
Anyway, I suspect you never want lines to cross. That means if you have slices A-F and anchors 1-6 some possible candidate arrangements are {A1, B2, ...F6}, {A2, C3, ..., E6, F1}, etc. through {A6, B1, ..., F5}, but you know {A1, B3, C2, ...} is going to be bad because it means lines will cross. ("Cross" is a simplification, but I think the "bad" probably generally applies.)
That means you only have n possibilities to try.
-
Start with the smallest slices first and place the labels for those, because they give you the least freedom. After that, you can use the existing label positions and the freedom that the current slice gives you to find a nicely spaced position for each successive label.
Greatly oversimplified, but I think it would make a good starting point.
-
Start with the smallest slices first and place the labels for those
That was my first thought, too.
-
Good ideas, guys.
Increasing the number of anchors beyond the number of slices also seems to help minimize conflicts, though occasionally lines still cross.
-
I have the sudden urge to play Simon.
-
-
It don't work.
Specifically: it works exactly 1 turn. You invariably lose the second turn. But it only flashes one color on the second turn instead of two, so...
-
-
It don't work.
Specifically: it works exactly 1 turn. You invariably lose the second turn. But it only flashes one color on the second turn instead of two, so...
No repro, though I grant you it's not as visible as it should be. It was more about playing with SVG, and the shape is actually generated from XSL.
-
It's a UI issue.
It does do the pattern the second time, but there's no graphical "division" between the button activating because I clicked it, and the button activating because it's the first button of the second turn.
-
I originally had the tiles laid out horizontally. I was surprised that when I wrapped them around radially, my brain was able to handle many more tiles.
The Simon game was more of a personal experiment than anything I ever intended to share. The Tetrominoes game is a bit more polished and ready for human consumption. Though people still complain they can't figure out the controls, and it doesn't do touch.
-
Or maybe some Tetr...ominoes.
You owe me new underwear and possibly new ear drums (I'll let you know once they stop ringing).
-
You owe me new underwear and possibly new ear drums (I'll let you know once they stop ringing).
I forgot I added the music in, it was the last thing I did. I rarely have speakers even attached to my computers.
-
No repro, though I grant you it's not as visible as it should be.
It worked for me too, though the difference between lit and unlit was way too low. I also missed not having the sound... makes it rather harder. Though not sure how well it'd work with so many buttons.
-
It seems like the best thing to do is to look at the sum of all lengths for all possible mappings and select the combination with the smallest total line length. Except that seems like it would be O(n!) (factorial) time.
Premature optimization is the root of all evil. Are you ever going to use this with n so large that the amount of time it takes to run is a problem?
-
No repro,
On the 2nd turn the first color doesn't reflash (at least not long enough to tell wtf is happening).
If you make the leap of faith about how to play, then it works fine from turn 3 on.
-
Premature optimization is the root of all evil. Are you ever going to use this with n so large that the amount of time it takes to run is a problem?
12! = 479,001,600
Yes.
Edit: Though I think it may be merely quadrilinear.
-
-
If rotating the pie chart could make the slices line up to anchors better, I would love to do that, but I really have no idea how to determine programatically whether rotation would be helpful, let alone how much.
The aim would be to put the largest slice at the top, the second largest at the bottom, and then to fill in on the sides trying to balance the weights (i.e., insert in the side which leaves things most balanced). It'd be at least relatively simple to do and O(N) after the initial sort.