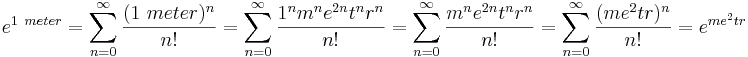An exercise in mathiness
-
Here is a Java exercise from a certain Java textbook (I don't actually know the title or author, since all I got was this photocopy). Try to figure out how many things are wrong with it (I count at least three).

-
The real question is, where the fuck did those numbers come from? At first I thought that they might have done something stupid like printed the sine, cosine, and tangent and labeled then arcsin, arccos, and arctan. Then I saw that arccos is 1.02 so that can't be the cosine of anything. Sigh, textbooks.
-
The sad part is that I actually figured out how they got those numbers. I was hoping someone would figure it out.
Here goes:
1) convert the user's input into radians2) use that radian value as an INPUT to the arc* functions
3) bash head repeatedly
-
Proving once again that those that can't do, teach.
-
@shill said:
The sad part is that I actually figured out how they got those numbers. I was hoping someone would figure it out.
Here goes:
1) convert the user's input into radians2) use that radian value as an INPUT to the arc* functions
3) bash head repeatedly
Wait, how does bashing your head result in the numbers? I understood 1) and 2)...
This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc. This shouldn't compile at all and give an error like "ERROR: Cannot perform inverse trigonometry on parameters with units." "ERROR, cannot add value with units 'a' to value with units 'b' ." "ERROR: Cannot assign value with units 'q' to value with units 'r' ."
Actually, it would be nice if the universe could throw errors like "FATAL ERROR: Continued attempts to perform <insert activity here> without sufficient ability" more often. (So far, the universe is only good at throwing those errors with high-powered applicances and/or sharp objects.)
-
@too_many_usernames said:
This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
Except you'll get fucked by units that aren't really units, like degrees, radians, decibels, etc.
-
@Welbog said:
you'll get fucked by units that aren't really units, like degrees, radians, decibels, etc.
How are degrees not really units?
-
@too_many_usernames said:
Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
No.
log(5 meters)-log (2 meters) = log(5/2).
-
Dang forum kept refusing to accept my update!
@Welbog said:
@too_many_usernames said:
This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
Except you'll get f****d by units that aren't really units, like degrees, radians, decibels, etc.Eh, radians is just a name, it's not a unit. Well, technically 'radians' is the same thing as the 'unitless' unit (whee!). Degrees is definitely a unit though. The distinction: you can raise a number to a power in radians, but you can't raise a number to a power in degrees. Oddly enough, this is why you can't use units in the inverse trig functions, because those are just exponentials.
Decibels...well, thinking about if that's a unit or not will take more brainpower than I want to expend right now on my lunch break.
@aka said:
No.
log(5 meters)-log (2 meters) = log(5/2).
Commence the banging of heads on tables. HINT: that is not a valid equation.
Edit: Another hint: log(5) - log(2) = log(5 meters / 2 meters) is valid.
-
@Welbog said:
@too_many_usernames said:
This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
Except you'll get fucked by units that aren't really units, like degrees, radians, decibels, etc.I don't know what's meant by "unit attributes". Hopefully he's talking about creating named types such as Degree, Radian, Decibel.
<font face="courier new,courier">Radian arctan(double);</font>
<font face="courier new,courier">double tan(Radian);</font>
<font face="courier new,courier">double tan(Degree);</font>
<font face="courier new,courier">Degree radianToDegree(Radian);</font>
<font face="courier new,courier">Radian degreeToRadian(Degree); </font>
-
@savar said:
I don't know what's meant by "unit attributes". Hopefully he's talking about creating named types such as Degree, Radian, Decibel.
<font face="courier new,courier">Radian arctan(double);</font>
<font face="courier new,courier">double tan(Radian);</font>
<font face="courier new,courier">double tan(Degree);</font>
<font face="courier new,courier">Degree radianToDegree(Radian);</font>
<font face="courier new,courier">Radian degreeToRadian(Degree); </font>
Nope, not talking about named types because you'd have to overload every math operator for every combination of units. What I'm talking about is an attribute associated with numeric values. Consider something like this (C++ style syntax - and I can't remember throws syntax at the moment as I've been stuck in embedded-C land and am too lazy to look it up - but it should be clear what I mean anyway):
class ValueWithUnits{ double val; String unit; ValueWithUnits& operator=(ValueWithUnits&) throws UnitsMismatchError; ValueWithUnits& operator+(ValueWithUnits&) throws UnitsMismatchError; ValueWithUnits& operator*(ValueWithUnits&); //and so on ValueWithUnits() { val = 0; unit = ""; } };ValueWithUnits& operator=(ValueWithUnits& rvalue)
{
if(unit != rvalue.unit) // units must be equal!
throw new UnitsMismatchError;
else
val = rvalue.val;
return *this;
}ValueWithUnits& operator*(ValueWithUnits& term)
{
units += "-" + term.units; // multiplcation combines units
value *= term.value;
return *this;
}
-
@too_many_usernames said:
@aka said:
No.
log(5 meters)-log (2 meters) = log(5/2).
Commence the banging of heads on tables. HINT: that is not a valid equation.
Edit: Another hint: log(5) - log(2) = log(5 meters / 2 meters) is valid.
What on earth are you talking about? It's perfectly well-defined.
-
Holy crap the edit timer is short:
Yes, I do realize that the code I wrote for operator* is really the code for operator*=.... but that's largely irrelevant for the point I was making.
By the way, aka, if you can tell me what exactly e^(1 meter) equals, then I'll accept that log(5 meters)-log(2 meters) = log(5/2) might be valid.
HINT: e^(1 meter) equals neither 2.71828... nor 2.71828... meters.
-
@too_many_usernames said:
Holy crap the edit timer is short:
Yes, I do realize that the code I wrote for operator* is really the code for operator*=.... but that's largely irrelevant for the point I was making.
By the way, aka, if you can tell me what exactly e^(1 meter) equals, then I'll accept that log(5 meters)-log(2 meters) = log(5/2) might be valid.
HINT: e^(1 meter) equals neither 2.71828... nor 2.71828... meters.
Surprisingly, e^(1 meter) equals 1/e^(-1 meter). But your question is beside the point, as a definition
of exp(unit) isn't required in the above equation at all, not even one of exp(log(unit)), one merely requires
that exp(-log(unit))*exp(log(unit))=1. Which is, of course, the whole point. Let me rephrase that:
HINT: this is, of course, the whole point.
And that's why people of substantial erudition routinely use log(...) - log(...) in numerical code and
get away with it.
-
@aka said:
Surprisingly, e^(1 meter) equals 1/e^(-1 meter). But your question is beside the point, as a definition
of exp(unit) isn't required in the above equation at all, not even one of exp(log(unit)), one merely requires
that exp(-log(unit))*exp(log(unit))=1. Which is, of course, the whole point.
Which is, of course, total and utter nonsense (except that indeed a definition of exp(unit) isn't required but a definition of log(unit)).@aka said:
Let me rephrase that:
HINT: this is, of course, the whole point.
And that's why people of substantial erudition routinely use log(...) - log(...) in numerical code and
get away with it.
Mathematical functions have a strong tendency to take dimensionless arguments, and I have yet to meet or read a paper by a person of even mediocre, let alone substantial, erudition who would even write something like
"log(5 metres) - log(2 metres)" except as a quotation. The thought that somebody would routinely do that is terrifying.
-
@aka said:
Surprisingly, e^(1 meter) equals 1/e^(-1 meter).
...
And that's why people of substantial erudition routinely use log(...) - log(...) in numerical code and
get away with it.
I will grant that log(a unit_a)-log(b unit_b) = log(a/b) works as a special case when unit_a and unit_b are identical; it does not work for arbitrary units.
So I suppose this means that we're both right and both wrong as neither of us fully specified the constraints on our statements.
That lack of specification is the error that causes things to fail the most often in my observation.
-
How are degrees not units?
With degrees, radians, and decibels, either the standard units involved cancel out, or were never involved in the first place. Radians, for example, are derived units, whereas kilograms are not. Calculation of decibel values involves ratios of logs in which the units cancel out. A degree is 1/360 of a circle's diameter--but no particular circle, because there's no such thing as a 'standard circle,' where there IS such a thing as a 'standard kilogram' or 'standard meter.'
-
@Ilya Ehrenburg said:
@aka said:
Surprisingly, e^(1 meter) equals 1/e^(-1 meter). But your question is beside the point, as a definition
of exp(unit) isn't required in the above equation at all, not even one of exp(log(unit)), one merely requires
that exp(-log(unit))*exp(log(unit))=1. Which is, of course, the whole point.
Which is, of course, total and utter nonsense (except that indeed a definition of exp(unit) isn't required but a definition of log(unit)).@aka said:
Let me rephrase that:
HINT: this is, of course, the whole point.
And that's why people of substantial erudition routinely use log(...) - log(...) in numerical code and
get away with it.
Mathematical functions have a strong tendency to take dimensionless arguments, and I have yet to meet or read a paper by a person of even mediocre, let alone substantial, erudition who would even write something like
"log(5 metres) - log(2 metres)" except as a quotation. The thought that somebody would routinely do that is terrifying.Oh. So, what is integral[x1..x2] dx/x?
-
@aka said:
Oh. So, what *is* integral[x1..x2] dx/x?
Provided x1 and x2 are positive real numbers, it's log(x2) - log(x1), which of course equals log(x2/x1). With a few caveats this also holds for nonzero complex numbers. But what's that to do with the price of beer? There are no units or dimensions involved.
-
@Ilya Ehrenburg said:
@aka said:
Oh. So, what *is* integral[x1..x2] dx/x?
Provided x1 and x2 are positive real numbers, it's log(x2) - log(x1), which of course equals log(x2/x1). With a few caveats this also holds for nonzero complex numbers. But what's that to do with the price of beer? There are no units or dimensions involved.
Noooooo...how would they. Never, since the inception of the world, has there been a need to do an integral over
a dimensionful quantity. -- Why don't you google for, say, '"log T" + Fermi' and be surprised about the amount of
mediocrity...
-
Okay, so apparently physicists do that. I stand corrected, as there certainly are a number of very erudite physicists.
-
@Ilya Ehrenburg said:
@aka said:
In that case, you're really going to be unhappy when you hear about imaginary numbers...Surprisingly, e^(1 meter) equals 1/e^(-1 meter). But your question is beside the point, as a definition
of exp(unit) isn't required in the above equation at all, not even one of exp(log(unit)), one merely requires
that exp(-log(unit))*exp(log(unit))=1. Which is, of course, the whole point.
Which is, of course, total and utter nonsense (except that indeed a definition of exp(unit) isn't required but a definition of log(unit)).@aka said:
Let me rephrase that:
HINT: this is, of course, the whole point.
And that's why people of substantial erudition routinely use log(...) - log(...) in numerical code and
get away with it.
Mathematical functions have a strong tendency to take dimensionless arguments, and I have yet to meet or read a paper by a person of even mediocre, let alone substantial, erudition who would even write something like
"log(5 metres) - log(2 metres)" except as a quotation. The thought that somebody would routinely do that is terrifying.
-
@Ilya Ehrenburg said:
@aka said:
Oh. So, what is integral[x1..x2] dx/x?
Provided
x1 and x2 are positive real numbers, it's log(x2) - log(x1), which of
course equals log(x2/x1). With a few caveats this also holds for
nonzero complex numbers. But what's that to do with the price of beer?
There are no units or dimensions involved.@aka said:
...stuff about integrating dimensionful numbers
Ok, consider the physical area of the graph of y = 1/x where y and x are dimensions, say meters. This means the formula is really y (in meters) = 1 m^2 / x (in meters) - this is the only way the units work out. Given:
Area = integral[x1..x2] ( 1m^2 / x dx)
This works out to
1 m^2 * integral[x1..x2] ( 1/x dx) = 1 m^2 * (log(x2) - log(x1)).
Note this illustrates that the log terms must be dimensionless because the units come solely from the scaling constant.
Yes, physicists often use the logarithm expression about which we're conversing, but they don't "get away" with anything: they correctly keep track of where the units are in their equations.
Consider if instead of a symbol for units we used a number. Let's then define a type of number 'distance' D = d * u where 'd' is the magnitude of the distance (a 'pure' number) and 'u' is some arbitrary nonzero number (doesn't even have to be real) which represents meters.
So for our area integral where x1 and x2 are distances, we really have:
Area = 1m^2 * ( log(x2)-log(x1) ) = 1m^2 * ( log(d2*u) - log(d1*u) ) = 1m^2 * (log(d2)+log(u) - log(d1)-log(u) ) = 1m^2*(log(d2/d1) - log(u/u)) = 1m^2*(log(d2)-log(d1))
So, since a unit is really just a unitless scaling factor with a specific meaning, the transcendental functions really do just take unitless numbers.
I'll leave it as an exercise for the readers to show how thinking of units as a scaling factor works for addition and multiplication as well.
-
@aka said:
Should have made the example more interesting like:@too_many_usernames said:
Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
No.
log(5 meters)-log (2 meters) = log(5/2).
log(5 meters) - log (2 centimeters) = ?
-
@mrprogguy said:
A degree is 1/360 of a circle's <font color="#ff0000">diameter</font>--but no particular circle
WTF?
-
@too_many_usernames said:
@Ilya Ehrenburg said:
And yet we're still not any closer to figuring out what too_many_usernames' avatar is.@aka said:
Oh. So, what *is* integral[x1..x2] dx/x?
Provided x1 and x2 are positive real numbers, it's log(x2) - log(x1), which of course equals log(x2/x1). With a few caveats this also holds for nonzero complex numbers. But what's that to do with the price of beer? There are no units or dimensions involved.
@aka said:
...stuff about integrating dimensionful numbers
Ok, consider the physical area of the graph of y = 1/x where y and x are dimensions, say meters. This means the formula is really y (in meters) = 1 m^2 / x (in meters) - this is the only way the units work out. Given:
Area = integral[x1..x2] ( 1m^2 / x dx)
This works out to
1 m^2 * integral[x1..x2] ( 1/x dx) = 1 m^2 * (log(x2) - log(x1)).
Note this illustrates that the log terms must be dimensionless because the units come solely from the scaling constant.
Yes, physicists often use the logarithm expression about which we're conversing, but they don't "get away" with anything: they correctly keep track of where the units are in their equations.
Consider if instead of a symbol for units we used a number. Let's then define a type of number 'distance' D = d * u where 'd' is the magnitude of the distance (a 'pure' number) and 'u' is some arbitrary nonzero number (doesn't even have to be real) which represents meters.
So for our area integral where x1 and x2 are distances, we really have:
Area = 1m^2 * ( log(x2)-log(x1) ) = 1m^2 * ( log(d2*u) - log(d1*u) ) = 1m^2 * (log(d2)+log(u) - log(d1)-log(u) ) = 1m^2*(log(d2/d1) - log(u/u)) = 1m^2*(log(d2)-log(d1))
So, since a unit is really just a unitless scaling factor with a specific meaning, the transcendental functions really do just take unitless numbers.
I'll leave it as an exercise for the readers to show how thinking of units as a scaling factor works for addition and multiplication as well.
-
@DOA said:
And yet we're still not any closer to figuring out what too_many_usernames' avatar is.
It's a moon ...
-
@bjolling said:
@DOA said:
And yet we're still not any closer to figuring out what too_many_usernames' avatar is.
It's a moon ...That's no moon, it's a space station!
-
-
@aka said:
@too_many_usernames said:
Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
No.
log(5 meters)-log (2 meters) = log(5/2).
Saying that is the equivalent of saying:
(1/0) / (1/0) = 1
You take the formula: x/x = 1, but then ignore the constraint: {x != 0}. In any equation, if a single thing is undefined, then the whole equation is undefined.
-
@amischiefr said:
@bjolling said:
*groan*@DOA said:
That's no moon, it's a space station!And yet we're still not any closer to figuring out what too_many_usernames' avatar is.
It's a moon ...
-
@DOA said:
*groan*
Oh come on man! Just like with fashion when bell bottoms came back in the late 90's, it has become cool once again to like Star Wars!@!! Horray for still living with mom!!
-
@amischiefr said:
it has become cool once again to like Star Wars!
You say that as if it was ever cool to like Star Wars in the first place.
-
@bstorer said:
@amischiefr said:
it has become cool once again to like Star Wars!
You say that as if it was ever cool to like Star Wars in the first place.What is _not_ cool about going to conventions? What is _not_ cool about living with mom (everybody love mom right?)? What is _not_ cool about being an overweight bald man in his mid 40's wearing a t-shirt that says "Wookies Rule!"? Good god, what are you a nerd?
-
@amischiefr said:
What is not cool about being an overweight bald man in his mid 40's wearing a t-shirt that says "Wookies Rule!"?
The fact that it's misspelled.
-
@DOA said:
It's obviously the wireframe of a sphere with a certain portion of the sphere covering slighly less than ⅛ of the surface area textured on the inside with a gradient that runs from pure lime green at the bottom to pure fire red at the top, viewed at an angle such that most of the red portions of the one-sided hull are not visible.And yet we're still not any closer to figuring out what too_many_usernames' avatar is.
What it represents, I have no f***ing clue.
-
@tster said:
@aka said:
@too_many_usernames said:
Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
No.
log(5 meters)-log (2 meters) = log(5/2).
Saying that is the equivalent of saying:
(1/0) / (1/0) = 1
You take the formula: x/x = 1, but then ignore the constraint: {x != 0}. In any equation, if a single thing is undefined, then the whole equation is undefined.
Right, I did not consider that. So it would be like saying that 5m/2m=5/2? Which is obviously nonsensical, what with meters being undefined and all?
-
No, log(metres) is undefined. You can multiply and divide units, raise them to fractional powers, no problem. Transcendental functions are a problem, however, the fact that physicists write things like log T when it should properly be log (T/K) notwithstanding ('kay, we mathematicians are sloppy in our notation, too, just in other ways).
-
@too_many_usernames said:
Ok, consider the physical area of the graph of y = 1/x where y and x are dimensions, say meters. This means the formula is really y (in meters) = 1 m^2 / x (in meters) - this is the only way the units work out. Given:
Naw, it works just fine with units inside the log, as long as you apply them consistently. Let:Area = integral[x1..x2] ( 1m^2 / x dx)
This works out to
1 m^2 * integral[x1..x2] ( 1/x dx) = 1 m^2 * (log(x2) - log(x1)).
Note this illustrates that the log terms must be dimensionless because the units come solely from the scaling constant.
Yes, physicists often use the logarithm expression about which we're conversing, but they don't "get away" with anything: they correctly keep track of where the units are in their equations.
Consider if instead of a symbol for units we used a number. Let's then define a type of number 'distance' D = d * u where 'd' is the magnitude of the distance (a 'pure' number) and 'u' is some arbitrary nonzero number (doesn't even have to be real) which represents meters.
So for our area integral where x1 and x2 are distances, we really have:
Area = 1m^2 * ( log(x2)-log(x1) ) = 1m^2 * ( log(d2*u) - log(d1*u) ) = 1m^2 * (log(d2)+log(u) - log(d1)-log(u) ) = 1m^2*(log(d2/d1) - log(u/u)) = 1m^2*(log(d2)-log(d1))
So, since a unit is really just a unitless scaling factor with a specific meaning, the transcendental functions really do just take unitless numbers.
I'll leave it as an exercise for the readers to show how thinking of units as a scaling factor works for addition and multiplication as well.
y := (1 m2) / x
A := int[x1 .. x2] y dx
x1 := 2 ft, x2 := 3 ft
Then:
A = int[2 ft .. 3 ft] (1 m2) / x dx
A = (1 m2) int[2 ft .. 3 ft] 1 / x dx
A = (1 m2) ( log(3 ft) - log(2 ft) )
A = (1 m2) ( log(3) + log(1 ft) - log(2) - log(1 ft) )
A = (1 m2) ( log(3) - log(2) ) =~ 0.405465108 m2
What may have confused you is the specific function you picked, and in particular the fact that int[ac .. bc] 1/x dx = int[a .. b] 1/x dx for any positive constant c. Thus, as long as both endpoints are in the same units, the units for the result indeed do come only from the integrand, since the ones from the endpoints cancel out.
Let's make it a little more interesting. Let y and A be defined as above, but let:
x1 := 10 in, x2 := 1 ft
Then:
A = int[10 in .. 1 ft] (1 m2) / x dx
A = (1 m2) int[10 in .. 1 ft] 1 / x dx
A = (1 m2) ( log(1 ft) - log(10 in) )
A = (1 m2) ( log(1) + log(1 ft) - log(10) - log(1 in) )
Now (belatedly) apply the fact that 1 ft = 12 in:
1 ft / 12 in = 1
log(1 ft / 12 in) = 0
log(1 ft) - log(12 in) = 0
log(1 ft) - log(12) - log(1 in) = 0
log(1 ft) - log(1 in) = log(12)
and therefore:
A = (1 m2) ( log(1) - log(10) + log(12) ) =~ 0.182321557 m2
which, indeed, you can verify by converting everything to meters and redoing the calculation that way. Of course, that will not be quite as convenient for these particular input values, since you'll have to work with multiples of 0.0254 meters rather than in round feet and inches. Still, my actual point wasn't that this would be a particularly convenient way to calculate such things, but merely that one can carry the units inside the logarithms all the way to the end if one wants to. In particular, if one didn't happen to know how many inches there are to a foot (Who uses such archaic units, anyway?), a perfectly reasonable answer would've been A =~ log(1 ft / 1 in) m2 - log(10) m2.
-
e^(1 meter), by Taylor expansion, would have to equal 1 unit plus 1 meter plus 1/2 a square meter plus 1/6 a cubic meter plus...
If anyone's building a spaceship in a Hilbert space or something that might be useful :)
This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
Units attributes tied to each value would cost a substantial amount of extra memory and CPU power. There's no good reason to include such a feature in a programming language unless it's for a computer algebra system. In reality, the programmer will know he/she did something wrong when the program doesn't work :)
Except you'll get [laid] by units that aren't really units, like degrees, radians, decibels, etc.
Decibels certainly are units. Degrees are deprecated and should not be used for future development.
-
@bstorer said:
Your pastimes include trolling a programming forum on the internet. Clearly, you're a man whose opinion of "cool" and "not cool" really matters.@amischiefr said:
it has become cool once again to like Star Wars!
You say that as if it was ever cool to like Star Wars in the first place.
-
@joeyadams said:
e^(1 meter), by Taylor expansion, would have to equal 1 unit plus 1 meter plus 1/2 a square meter plus 1/6 a cubic meter plus...
If anyone's building a spaceship in a Hilbert space or something that might be useful :)
It's beginning to dawn on me that most people seem to be victim of a sub-prime science education. Quantities don't "have" units. 'm' in 'exp(17m)' is a mere tag, it's a reminder that that particular number came about by having to lay 17 meter-long rods end-to-end to match the length of the object. We always form exponentials of numbers.
Systems of measurement are arbitrary, but a general statement such as 'area=length*height' should not depend on the system chosen. 'Dimensional analysis' is just that: making sure we're not dealing with statements that are true by mere coincidence by checking their independence of the system of units.
As long as one is dealing with sums, products, and fractions, this can be done by treating the tags on the same footing as positive real constants, multiply them, raise them to powers, and reduce fractions. In the end, one checks for algebraic homogeneity. That works so well in practice that people hypostasize mysterious algebraic objects named "Meter", "Volt" and "Ampere" (stored in an underground Banach space in Paris, I assume).
Now, it's easy to check that log(length/height) = log(length) - log(height) holds independent of the measuring rods one happens to use for length and height. It's just not possible to check by inspecting just one term of the sum (say, log(length)). Well, of course not. Logarithms turn products into sums. But for some reason, this deeply upsets people; much more than the fact that they cannot dimension-check 'area=length*height' by looking at 'height' alone.
-
@merreborn said:
Your pastimes include trolling a programming forum on the internet. Clearly, you're a man whose opinion of "cool" and "not cool" really matters.
As opposed to you: a sad, humorless wretch whose life consists of such crushing disappointment that you must grasp desperately at opportunities to swell with righteous indignation in the hopes that others will join you in your ire, because that is the only time you aren't alone. Look, as big as it must make you feel to show the scary troll that you aren't afraid, perhaps next time you can save it for a post wherein I do anything remotely trollish? Star Wars is for nerds. I don't think this is any great secret.
-
@vyznev said:
... stuff
I'm a bit confused... isn't this identical to the post of mine which you quoted? I agree that you can carry the units around inside the logs so long as they are consistent and end up becoming unitless at the end.
I think maybe I need to better state the intent of my long late-night post: If you think of a unit as a variable instead of something magical, then even operating on a unit is like operating on a unitless number.
-
@joeyadams said:
Units attributes tied to each value would cost a substantial amount of extra memory and CPU power. There's no good reason to include such a feature in a programming language unless it's for a computer algebra system.
I agree that if you make sure the equation is correct the programming language doesn't need the semantic baggage. Apparently, though, many people are not capable of ensuring their equations are set up correctly.
I'm not actually advocating making programming languages that do this to prevent people from making dumb mistakes; I like it when poor decisions have adverse ramifications.
-
@too_many_usernames said:
@vyznev said:
Oh, ok... I must've gotten confused about who was arguing for what position. Sorry. We seem to be in violent agreement, then. :)... stuff
I'm a bit confused... isn't this identical to the post of mine which you quoted? I agree that you can carry the units around inside the logs so long as they are consistent and end up becoming unitless at the end.I was mostly taking issue with the bit where you wrote that "... this illustrates that the log terms must be dimensionless because ...", which sounded like you were saying that expressions like log(1 meter) are invalid or not defined (like 1/0, which someone compared them to above). The point of my example was to show that they are perfectly valid expressions, even if we don't know their numeric value, and may be used just like any other expression containing an unknown term.
@too_many_usernames said:
I think maybe I need to better state the intent of my long late-night post: If you think of a unit as a variable instead of something magical, then even operating on a unit is like operating on a unitless number.
Well, that I can certainly agree with.(BTW, an exercise in advanced dimensional analysis, for interested readers: From my example above, it also follows that int[1 m .. 2 m] (1 m2)/x dx = log(2) m2 = int[1 kg .. 2 kg] (1 m2)/x dx. Explain. Why is the same not true for int[1 m .. 2 kg] (1 m2)/x dx?)
-
@too_many_usernames said:
I agree that if you make sure the equation is correct the programming language doesn't need the semantic baggage. Apparently, though, many people are not capable of ensuring their equations are set up correctly.
I suppose a language that did dimensional analysis (preferably at compile time) for numeric values could be useful for engineering etc., but what I'd really like to see would be a language that did similar analysis for strings, such that e.g. concatenating random user input with an SQL statement would be immediately flagged as an error, just as if you were adding meters and kilograms together in normal dimensional analysis.I'm not actually advocating making programming languages that do this to prevent people from making dumb mistakes; I like it when poor decisions have adverse ramifications.
-
@vyznev said:
"... this illustrates that the log terms must be dimensionless because ...", which sounded like you were saying that expressions like log(1 meter) are invalid or not defined (like 1/0, which someone compared them to above).
Yeah, I think a better way to have phrased that would have been "this illustrates that log terms must evaluate to being dimensionless" in those types of situations. Just a log(units) by itself technically has a strange unit, but isn't terribly useful. However, since the logarithm must have a definition equivalent to its integral definition, I'm not sure you can actually have a log(units) by itself in practice (since the integral definition 'normalizes' the units)...but I admit that's beyond my understanding of mathematics.
(BTW, an exercise in advanced dimensional analysis, for interested readers: From my example above, it also follows that int[1 m .. 2 m] (1 m2)/x dx = log(2) m2 = int[1 kg .. 2 kg] (1 m2)/x dx. Explain. Why is the same not true for int[1 m .. 2 kg] (1 m2)/x dx?)
I wonder how many will be kept up late wondering about that one =)
-
@vyznev said:
I suppose a language that did dimensional analysis (preferably at compile time) for numeric values could be useful for engineering etc.
You can do that in C++, if you build the framework. Though I'm sure there is one already.
-
@joeyadams said:
Point is, it doesn't matter: it works, that polynomial is a well-defined and manageable thing, even more so than i (sqrt -1).e^(1 meter), by Taylor expansion, would have to equal 1 unit plus 1 meter plus 1/2 a square meter plus 1/6 a cubic meter plus...
If anyone's building a spaceship in a Hilbert space or something that might be useful :)
I don't understand why anyone's having such a problem with this.
If you can happily treat the square root of minus one as an unknown and sling it around in complex equations, let it cancel out, and otherwise algebraically manipulate it, you should have no problem with the concept of the log of 1 meter. In an equation like log(5m) - log (2m) the whole polynomial will behave as a term and can be manipulated: let X = the polynomial for log(1 meter), then you can see how it's fine to write log (5m) as log(5) + log(m) === X + log(5) and the equation becomes (X + log 5) - (X + log 2) or (log 5 - log 2) or log (5/2) as first stated; all the terms in the polynomial cancel out.
@joeyadams said:This is why math functions should always have 'units' attributes. Certain functions are only valid on unitless parameters, like inverse trig functions, logarithms, etc.
Units attributes tied to each value would cost a substantial amount of extra memory and CPU power. There's no good reason to include such a feature in a programming language unless it's for a computer algebra system. In reality, the programmer will know he/she did something wrong when the program doesn't work :)
Units wouldn't be done as attributes, you'd use the language's type system to implement them.
@joeyadams said:
WTF? Decibels are a dimensionless ratio. Degrees are a physical unit like radians.Except you'll get [laid] by units that aren't really units, like degrees, radians, decibels, etc.
Decibels certainly are units. Degrees are deprecated and should not be used for future development.