Patterns of Primes
-
The mathematicians made the discovery while performing a randomness check on the first hundred million primes. Within that set, a prime ending in 1 is followed by another ending in 1 just 18.5 percent of the time. That shouldn’t happen if they were truly random—we should expect to see this happen 25 percent of the time (keep in mind that primes can only end in 1, 3, 7, or 9). So while this isn’t a pattern—it’s also not totally perfectly random. In terms of the back-to-back distribution of the other numbers, primes ending in 3 and 7 appeared 30 percent of the time, and consecutive 9s appears about 22 of the time. Importantly, this observation has nothing to do with the base-10 numbering system, and is something inherent to primes themselves.
I find this very unpersuasive. They looked at an infinitesimal sample of primes and are trying to generalize an observation. Note that the article points this out a little later:
“As the numbers get larger, though, it sounds like this is less constraining, causing it to get closer and closer to an equal distribution of ending digits— which makes intuitive sense, since the primes get rarer and rarer,” he said.
I mean...it's an interesting pattern, but hardly surprising that a tiny sample ends up not being what you thought it would be. And yes, obviously the statement "keep in mind that primes can only end in 1, 3, 7, or 9" is wrong.
-
"keep in mind that primes can only end in 1, 3, 7, or 9"
if you exclude 2, and 5 from that statement as being "trivial" then it is accurate. ay even number has two as a divisor, so the only even number prime is 2, and any number ending in 5 must be divisible by 5 and so 5 is the only prime with a ones digit of 5.
it gets a lot more complicated from there, but those two at least are trivial, leaving you with 4 other end digits for primes, which if they were truely random you would expect to see account for about 25% each of the primes.
i'll agree with you that it's not necessarily indicative of a larger pattern, though it is interesting and i would be interested in seeing more research on the matter.
all i can say for certain right now is.... Primes are WEIRD!
take Ulam Spirals for instance:

there is clearly some organization there, some diagonals have a much denser population of primes than others, yet no one has been able to prove a reason why, just to say that "hey, there's a lot of primes on this diagonal, so let's look along the diagonal for new primes!"
-
"keep in mind that primes can only end in 1, 3, 7, or 9"
if you exclude 2, and 5 from that statement as being "trivial" then it is accurate. ay even number has two as a divisor, so the only even number prime is 2, and any number ending in 5 must be divisible by 5 and so 5 is the only prime with a ones digit of 5.
So you adjust your wording: "keep in mind that multi-digit primes can only end in 1, 3, 7, or 9".
-
What about 11? or 10? Those are both primes. 101 is also a prime. And 111.
-
-
there is clearly some organization there, some diagonals have a much denser population of primes than others,
The trouble with that argument is that the 'diagonals' are determined by how wide you draw the picture...
-
So are B and D, but they always get ignored, poor sods.
-
You can't feel too sorry for them though; they play starring roles in cryptography
-
And checksum codes, they love them for that.
-
The trouble with that argument is that the 'diagonals' are determined by how wide you draw the picture...
actually no, the diagonals are independant of the picture because of how ulam spirals are constructed
you build them this way:

so the diagonals are independant of the size of the spiral.
really the Ulam Spiral, is just a neat visualization of primes, a way to show that the primes are not randomly placed, but they are also not very predictably placed either. and the densely populated diagonals, which each have a specific mathematical formula for generating numbers along the spiral, are nothing more than a way of creating prime candidates that have a slightly better chance than average of being prime.
-
a way to show that the primes are not randomly placed, but they are also not very predictably placed either.
"Not predictably (given some set of knowledge)" seems like the very definition of random, though.
-
"Not predictably (given some set of knowledge)" seems like the very definition of random, though.
There are patterns in primes, far more than we would expect in a truly random set. but we don't know enough of the rules of that organization to predict with anything approaching certainty where primes will be.
Another famous example: Mersenne Primes. These are primes of the form
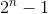 . We know a lot of interesting things about these numbers. For instance we can fairly trivially prove that if
. We know a lot of interesting things about these numbers. For instance we can fairly trivially prove that if 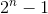 is prime then
is prime then nmust be prime.*As for the ulam spirals... I'll let James Grime, a PHD holding matematician try to explain it better while i go looking for more props.
Prime Spirals - Numberphile – 09:06
— Numberphile*a full proof of this and other neat properties of mersenne primes is available on wikipedia
-
There are patterns in primes, far more than we would expect in a truly random set.
Ah, the No True Random defense. Your still wrong. That the human brain, pattern detector par excellence, can detect patterns in randomness does not show that said randomness isn't random.
Another famous example: Mersenne Primes. These are primes of the form . We know a lot of interesting things about these numbers. For instance we can fairly trivially prove that if is prime then n must be prime.*
But not all Mersenne numbers are primes. Obviously, we know exactly how prime numbers "come about," but that's not the same thing as saying there's a predictable pattern.
-
But not all Mersenne numbers are primes.
this is true, in fact mersenne primes are relatively rare compared to what one would expect from a random sample. we look for them because they are a lot easier for computers to work with.
-
-
Importantly, this observation has nothing to do with the base-10 numbering system, and is something inherent to primes themselves.
Yes it does. For example:
What about 11? or 10? Those are both primes. 101 is also a prime. And 111.
There's never going to be a prime ending in anything other than
1(except10) in that base.
-
Ah, the No True Random defense. Your still wrong. That the human brain, pattern detector par excellence, can detect patterns in randomness does not show that said randomness isn't random.
Why is there always someone who says this whenever the Ulam spiral is posted? There are real, clear patterns there, you can measure it if you want. Or just look at some actual random dots and see that they look completely different.
-
Why is there always someone who says this whenever the Ulam spiral is posted?
Because I'm right?

I think you're substituting some other definition of random that the one I used in my argument.
-
Primes aren't random, because they're not selected but a fixed set. Insert XKCD
return 4meme hereA random selection can certainly have patterns If I have a random number generator that rejects even output, or doubles each number returned, then I have some random numbers with the pattern that they are all even.
-
Primes aren't random, because they're not selected but a fixed set. Insert XKCD return 4 meme here
:sigh:
I think you're substituting some other definition of random that the one I used in my argument.
"Not predictably (given some set of knowledge)" seems like the very definition of random, though.
-
Random != unpredictable
For instance, I cannot predict when an accident is going to shut down the westbound carriageway of the M62 between Leeds and Bradford, but it's not a random event either; it's more likely to happen when traffic levels are higher and/or the weather is bad.
-
so the diagonals are independant of the size of the spiral.
But the apparent diagonal lines in the spiral (visible in your earlier post) appear in locations that are rather difficult to predict. They're mostly not on the major diagonals, but the significance is baffling. It's like it ought to mean something, but who know what?
You could also analyse the spectrum of the feature sizes, and see if that looks random. Which would be rather hard to do for a large set of primes…
-
more likely to happen when
Random != uniform distribution.
Motorway accidents arguably aren't random, but not because there are times when they're more likely
-
I cannot predict when an accident is going to shut down the westbound carriageway of the M62 between Leeds and Bradford
That one's pretty easy: think “daily event” and you won't be too far off.
-
-
Hence the
arguablydistinction. We are getting to a point where everyone has their own definition of random now
-
everyone has their own definition of random now
Are they random definitions of random?
-
What about enter-enter slow-mo random definitions of random?
-
No, they're arbitrary
-
You're arbitrary.
-
They're random, you're arbitrary, I'm just hard to predict. ;)
-
Paging @SpectateSwamp
-
Random != unpredictable
For instance, I cannot predict when an accident is going to shut down the westbound carriageway of the M62 between Leeds and Bradford, but it's not a random event either; it's more likely to happen when traffic levels are higher and/or the weather is bad.
You're making my point for me and contradicting your first statement. Stuff looks more likely to be random the less you know about the causes.
-
Stuff looks more likely to be random the less you know about the causes.
Just because something looks random, doesn't mean it is random. Weather looks random (especially British weather), but it's actually totally deterministic; we just don't know all the variables.
-
-
Just because something looks random, doesn't mean it is random. Weather looks random (especially British weather), but it's actually totally deterministic; we just don't know all the variables.
They say the first rule of holes is, "When you're in one, stop digging."
quantum mechanics disagrees.
As far as we know.
-
-
-
They say the first rule of holes is, "When you're in one, stop digging."
But if I stop digging, how will I get to China?
-
-
That the human brain, pattern detector par excellence, can detect patterns in randomness does not show that said randomness isn't random.
The human brain, pattern inventor par excellence, is as capable of applying its ability to sort and categorize to randomness as to anything else. The Ulam spiral contains sub-patterns that are not present in, for example, a field of the same size where the decision about whether to color a dot is made on the basis of fair dice rolls; that makes it a different kind of randomness than, for example, TV snow.
Looked at another way, the Ulam spiral is not random at all; it's completely deterministic and completely predictable: its Kolmogorov complexity is very low, unlike that for any representative frame of TV snow.
-
As far as we know.
Something something Bell's theorem something something EPR paradox.
-
that makes it a different kind of randomness than, for example, TV snow.

Looked at another way, the Ulam spiral is not random at all: it's completely deterministic and completely predictable: its Kolmogorov complexity is very low, unlike that for any representative frame of TV snow.
Sure, we can predict primes. We might say that their distribution is not random at all, since we know exactly how to produce all of them less than
n. But we're talking about more than their distribution. We're talking about their relationship to each other, which I think is not identical to their identity.That there are patterns in one representation of them does not convince me of their non-randomness. As mentioned up thread, there are other patterns in random data. Instead of normally or exponentially or whateverly distributed, we could call these Ulam-spirally distributed.
-
-
Better hope you randomly walk onto a cross-channel ferry
-
@boomzilla said:
Random walk?
Across the English Channel? I'm not sure I have stilts that long...It's entirely possible that the walk leads you onto a boat or the Chunnel or a plane. Or takes long enough that we get an ice age and you can just walk across.
-
They're mostly not on the major diagonals, but the significance is baffling. It's like it ought to mean something, but who know what?
Patterns of various kinds turn up all over the place in collections of prime numbers. Fire up this little sieve toy and click all the primes in the top row; this gives you a grid highlighting all the primes below 900. There's plenty of "randomly" placed regularity in the result: all the vertical columns of white cells are examples of prime arithmetic progressions p = an + b where p is prime, n is successive integers starting from 0, and a and b identify the progression.
The white vertical columns on that map all have a = 30, and the longest columns (b = 7, 107, 359 and 541) have 6 elements. It was recently proved (2004) that prime arithmetic progressions of arbitrary length exist though as far as I know there is still no analytic method for finding those; the longest one currently known (found with a software search) is the 26-element sequence with a = 43142746595714191, b = 5283234035979900 for n in 0..25.
According to that Wikipedia article the proof was extended in 2006 to cover progressions where the spacing is defined by an arbitrary integer polynomial rather than a constant, which means that a sufficiently large Ulam spiral will feature arbitrarily long diagonal stripes.
In fact long stripes on the Ulam spiral seem rather easier to find than long stripes on a sequentially numbered grid.
-
@Jaloopa said:
everyone has their own definition of random now
Are they random definitions of random?
There's a certain amount of visible structure, but no general formula for predicting where it will manifest.
-
-
Weather looks random (especially British weather), but it's actually totally deterministic; we just don't know all the variables.
Weather involves processes with multiple feedbacks and is therefore inherently chaotic i.e. exquisitely sensitive to small alterations in initial conditions. And since some of the processes that set those initial conditions are chemical, and chemistry is most accurately described by quantum mechanics, and quantum mechanics is non-deterministic: weather is ultimately random.
 Mathematicians Discovered Something Super Freaky About Prime Numbers
Mathematicians Discovered Something Super Freaky About Prime Numbers


 Poisson distribution - Wikipedia
Poisson distribution - Wikipedia