:fa_bar_chart_o: Probability is confusing.
-
Yep, that was it: https://ideone.com/oQd31n
@anotherusername thank you very much.
-
Assuming that they croak randomly, there's a significantly higher chance that you'll hear a croak from the clearing if there are two male frogs in the clearing.
We could also assume that they croak when they see a female frog (which they can differentiate), as a mating call, in which case the chance of the other one being female is much higher.
-
This question actually ignores a very significant detail. What is the probability that a male frog croaks in the time you spent listening? Assuming that they croak randomly, there's a significantly higher chance that you'll hear a croak from the clearing if there are two male frogs in the clearing.
Ah! wow, it all makes sense now!

I modified my spreadsheet to run 100k trials, where the male frogs croak at a given probability, which I can change.
If the probability that male frogs will croak is low, then you're a lot more likely to hear a croak from the clearing if both frogs in the clearing are male. So if you heard a croak from the clearing (and not from the stump), the probability that one of the frogs in the clearing is female is closer to 50%...

But if the probability that male frogs will croak is high, then if you heard a croak from the clearing (and not from the stump), then it's less likely that both of those frogs are male, and the probability that one of them is female is closer to 2/3:
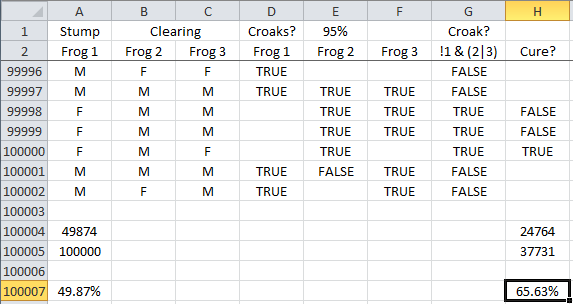
Also, the fact that you can't wait just a few seconds longer to see if the frog on the stump croaks would suggest that they croak less often, not more...
We could also assume that they croak when they see a female frog (which they can differentiate), as a mating call, in which case the chance of the other one being female is much higher.
True, but if there were no female frogs already within his eyesight, how would a male frog attract one?
-

-
The video specifically says you can lick both frogs in the clearing. You have to chose between going to the stump and licking one frog with a 50% chance of it being female, or going to the clearing and licking both frogs with one of them being male and other other being 50% chance female. Right?
If I have enough time to think about this, I probably have enough time to lick all three frogs.

-
I probably have enough time to lick all three frogs.
And then realize in horror that all of the frogs were male...
Shut up,
 Engine, I'm not that kinky!
Engine, I'm not that kinky!
-
Oh look a thread about Math...

-
I don't get one thing.
Combinations are MM, MF, FM, FF.
If you don't hear the croak, chances are 3/4.
If you hear the croak, it's just MM, MF, FM - chances are 2/3.
However, if you don't just hear the croak, but also see which of them croaked, then it's either MM, MF or MM, FM - in either case, chances are now 1/2.
IS THERE ANY LOGICAL EXPLANATION WHY WATCHING THE FROGS REDUCES OUR CHANCES OF SURVIVAL?
Because if there isn't, I call bullshit on this solution.
-
Combinations are MM, MF, FM, FF.
If you don't hear the croak, chances are 1/2.
You may want to check that again.
-
In other words - if I have a sequence of two elements in random order, where one is 0 and the other is either 0 or 1, then the probability of the latter being 1 depends on whether I removed the former from the sequence or not. This doesn't sound right.
-
-
IS THERE ANY LOGICAL EXPLANATION WHY WATCHING THE FROGS REDUCES OUR CHANCES OF SURVIVAL?
Because if there isn't, I call bullshit on this solution.
It's because the probabilities in each case are based on the information available at the time the probability is calculated. Each time you look at the available scenarios and determine the odds of finding what you need. As you gather more information, you are able to refine your calculations by eliminating possible scenarios.
-
It's still counter-intuitive. If you've got two frogs and you know one of them is male, but you do not know which, the chance of one of them being female is 2/3. If you know specifically which one is male, the chance of one being female is 1/2.
-
It's still counter-intuitive. If you've got two frogs and you know one of them is male, but you do not know which, the chance of one of them being female is 2/3. If you know specifically which one is male, the chance of one being female is 1/2.
That's probability for you. ¯\_(ツ)_/¯
-
Would you believe me if I told you the kind of Mathematicians most likely to have gambling problems are Statisticians?
-
IS THERE ANY LOGICAL EXPLANATION WHY WATCHING THE FROGS REDUCES OUR CHANCES OF SURVIVAL?
It's still counter-intuitive. If you've got two frogs and you know one of them is male, but you do not know which, the chance of one of them being female is 2/3. If you know specifically which one is male, the chance of one being female is 1/2.
Actually, I think the key is how you know one of the frog's gender. By definition, the "croaks = male" criteria can only tell you a frog is male; it can't reveal the gender of a female frog.
This isn't a situation of "the gender of one frog is revealed" (which would mean the gender of the other frog is 50/50), it's "the gender of one male frog is revealed". It doesn't make any difference if you see which frog croaks, or only hear it.
Anyway, in the simulation I ran, I was able to see which of the two frogs croaked and it didn't affect the outcome.

-
Knowing specifically that one of the frogs in the clearing is male removes that frog from the equation. Rather than MM, MF, and FM possibilities, we've only got MM and MF left.
-
Knowing specifically that one of the frogs in the clearing is male removes that frog from the equation.
That's only true if it was equally possible and likely for you to learn that one of the frogs was female.
It's exactly like the Monty Hall problem: the revealed door doesn't just drop out of the equation, because the person who opened it knew and only opened one one of the doors with a goat behind it. If he didn't know, then the probability of the remaining door having the prize would still be 1/3. (And there'd also be a 1/3 possibility that he opened the door with the prize, so you'd win by default.)
Rather than MM, MF, and FM possibilities, we've only got MM and MF left.
MF is twice as likely because the original possibilities were: both female (25%), both male (25%), one of each (50%).
-
IS THERE ANY LOGICAL EXPLANATION WHY WATCHING THE FROGS REDUCES OUR CHANCES OF SURVIVAL?
Yes, but it's not intuitive: your chances of survival aren't reduced. Your knowledge of your chances of survival is.
Let's take 1000 possible cases. Of these, about 250 will have the MM distribution, 250 the FM, 250 MF and 250 FF. If you only hear the croak but you don't see it, you immediately discard the FF, and so you can be in any of the remaining 750 possible universes. Of these, you die in 250 cases. 500 yous survive.
However, let's say you see the frog. So, the question then is, which one did you see? If you saw the first frog croak, you discard two distributions and are left with 500 cases that are split evenly between the MM or MF distributions. If you saw the second frog croak, you are then in either the MM or FM distributions. See how the MM distribution is repeated? That's what messes up your intuition. Over the whole 1000 cases, there are still 500 yous that live, 250 that saw the first frog croak and 250 that saw the second frog croak. 250 still die because the frog they didn't se croak was male too. And 250 are discarded because they didn't see any frog croak.
The extra information constrains the possible cases you can be in, not the underlying state of the situation.
-
That assumes that there's an equal likelihood of hearing frogs croak, which isn't true because females don't.
-
"That" what? You're going to have to be more specific.
-
"First frog", "second frog", where you assume that you see one or the other frog croak.
Since only a male frog can croak, it actually doesn't tell you anything more if you see which frog croaked. All you know is that, of the original 4 situations, FF is impossible.
Anyway, the proof is in the simulation. Like I already said, my simulation showed which of the frogs croaked, and the probability was still 2/3 that one of the two frogs was female.
-
Anyway, the
proofapproximation consistent with the logical but non-intuitive conclusion is in the simulation.FTFY.
-
I'm reasonably sure that my simulation correctly represented the entirety of the situation, which would make its consistent result a "proof", but I'm open to discussion if you think there's something I missed.
-
Anyway, the proof is in the simulation. Like I already said, my simulation showed which of the frogs croaked, and the probability was still 2/3 that one of the two frogs was female.
Your simulation is right, but it doesn't answer the question I was answering. The problem with relying on simulations is that you don't need to understand the problem.
If you check your data, you'll note that of the cases where clear1 was male, half result in death and half result in survival. Of the cases where clear2 was male, half result in death and half result in survival. Once you know which is the male, the information at your disposal is different, and different information constrains the possible cases you can be in in different ways.
So, if you ran 1000 people through the scenario, with the condition that they get to see the frog croak, 500 people are still going to come out saying that they saw a frog croak. But of those, 250 will say they saw one frog croak, and 250 will say they saw the other frog croak (250 will say they saw no frog croak, and 250 and don't make it out).
And if you think it doesn't matter if you see the frog croak, consider this change to the scenario: licking a male frog kills you instantly. Would you still think that knowing which frog croaked is irrelevant?
-
If you check your data, you'll note that of the cases where clear1 was male, half result in death and half result in survival. Of the cases where clear2 was male, half result in death and half result in survival. Once you know which is the male, the information at your disposal is different, and different information constrains the possible cases you can be in in different ways.
Like I said, that neglects the fact that only a male frog can give away its gender.
And if you think it doesn't matter if you see the frog croak, consider this change to the scenario: licking a male frog kills you instantly. Would you still think that knowing which frog croaked is irrelevant?
No, because that's a completely different scenario.
-
EVERY PROBABILITY PROBLEM IS CONDITIONAL
So, so, so, so, so much this.
But instead we are taught idiocy in schools... like "unconditional" probability and the insanity that relative frequencies are the same as probabilities. And that there is an actual way to select a "random" sample. And that randomness somehow grants magic powers to probability distributions. And that in order to have a probability, an event has to be repeated into infinity. Of course, there is only one 2016 election, so there is no probability that anyone will be elected. Even the Bayesians get into nonsense like priors which just makes one's head hurt
 .
.Generally I think Leibniz, Laplace (for the most part), and Keynes actually had a lot of it right. I blame Venn and Fisher for today.
-
Yes-No-Maybe
-
Gödel makes my head hurt even more.
-
Like I said, that neglects the fact that only a male frog can give away its gender.
And you were just as wrong when you said it the first time.
Knowing what frog croaked doesn't change the overall results. Out of 1000 cases, 500 hear a croak and live. That doesn't change no matter how you change the information available. You could paint the female frogs pink and you'd still have 500 people hear the croak and live and 250 hear the croak and die. The difference would just be that the 250 would know with 100% certainty that they're screwed when they see no pink frog, while the 500 that live would know with 100% certainty that they are going to live because they saw a pink frog.
But the question is, why did seeing the frog croak lower your chances? Since you don't like my answer, can you provide an explanation for the math?
-
Whoa, where has this thread gone? I thought we already established that even though MF/FM have to be counted separately, the order doesn't matter.
But the question is, why did
seeinghearing the frog croak lower your chances?Because it eliminates FF as a possibility? Or was that a rhetorical question?
-
But the question is, why did seeing the frog croak lower your chances
Imagine a slightly different problem:
It goes like this: you are poisoned and will die, but female frogs of a certain species can cure you. The male and female frogs are identical as far as you can tell except that only the male frogs have a distinctive croak.
You are between a stump and a clearing. On the stump is a frog of this species. In the clearing are 1000 frogs of this species. You then hear 999 distinctive croaks from 999 different frogs in the clearing. Now is when you have to decide: which way do you go for the best chances of survival?
Of course you'd go to the clearing!
Prior to hearing the croaks, you had a 1 in 2 chance of dying if you stay, and a (1/2)^1000 chance of dying if you go to clearing.
After hearing the croaks, you still have a 1 in 2 chance of dying if you stay, and a 1 in 1000 chance of dying if you go to the clearing (the FMMMMM.... to ...MMMMMF permutations, plus the MM..MM one).
So your chances of dying went up (or chances of living went down) a lot after hearing a croak. The same is true for the 2 frogs.
-
Knowing what frog croaked doesn't change the overall results.
Um... right. That's what I said.
the question is, why did seeing the frog croak lower your chances?
It didn't.
-
Actually, no, ignore that. I think I'm wrong. The bit I was missing is you can't distinguish frog1 and frog2. So even if you know which one is croaking, you could still be in either the MF or FM situation. It's only if you can distinguish them that your chance drops.
-
I'm not arguing against that. I'm saying that knowing that at least one is male isn't the same as knowing which is male.
You're saying the frogs being male or female are completely independent, based on things like coin flips, right?
So the statement of this problem is like:
You are poisoned and will die, but flipping a coin can cure you if it comes up tails. You can choose: Flip Coin A. Or flip Coin B and C, where C is two-headed.
You are saying that knowing that specifically coin C is two headed adds no information to Coin B, correct? And you would be right. In this problem, the probability space is:
Coin A: H > Death T > Cure Coin BC: HH > Death TH > Cure
Now, if the problem was (this is basically the frog problem):
You are poisoned and will die, but flipping a coin can cure you if it comes up tails. You can choose: Flip Coin A only, or flip Coins B and C. You choose to flip coins B and C for better chances of survival. Then, someone tells you that at least one of the two coins, B or C, is two headed, and asks if you want to change your choice.
Prior to your knowledge:
Coin A: H > Death T > Cure Coin BC: HH > Death TH > Cure HT > Cure TT > Cure
After your knowledge:
Coin A: H > Death T > Cure Coin BC: HH > Death TH > Cure HT > Cure [s]TT > Cure[/s]
You still want to flip both coins.
If we then add one additional piece of knowledge (that we don't have in the frog problem, since we don't see which frog croaked):
After you choose, someone then shows you Coin C, which is two headed, and asks if you want to change again.
Your probability space collapses.
Coin A: H > Death T > Cure Coin BC: HH > Death TH > Cure [s]HT > Cure[/s]
Now you have an equal chance to die.
Probability is all about information.
-
Anyway, in the simulation I ran, I was able to see which of the two frogs croaked and it didn't affect the outcome.

Here, I've updated the original simulation that...someone (@LB_?) posted:
It simulates the case of seeing which frog croaks. And the answer is 50%.
-
Wrong, because if you can see that one frog is male, you're back to the odds the other one is female, multiplied by the chance you're a dumbass who wastes time licking a frog he knows won't cure him, which in practice is 100% so you've got a 0% chance to survive.
-
I really wanted a goat anyways.
-
What diseases can licking a goat cure?
-
I imagine it could help clear out your sinuses. Possibly an alternative to getting one's stomach pumped?
-
Let's take 1000 possible cases. Of these, about 250 will have the MM distribution, 250 the FM, 250 MF and 250 FF. If you only hear the croak but you don't see it, you immediately discard the FF, and so you can be in any of the remaining 750 possible universes. Of these, you die in 250 cases. 500 yous survive.
The problem with this reasoning is that you assume that the possible universes are distributed equally between the four possible frog sets. What if out of 1000 universes, there were 960 such that both frogs are male?
-
Give me a question with some relevance in a real life situation instead of frog-licking or some game show that hasn't been on the air since like 1960, then maybe I'll pay attention.
Literally thousands of people have been wrongfully convicted of crimes because people don't understand conditional probability. Some of them have been executed.
https://en.wikipedia.org/wiki/Prosecutor's_fallacy
Do we have your attention now?
-
The problem with this reasoning is that you assume that the possible universes are distributed equally between the four possible frog sets. What if out of 1000 universes, there were 960 such that both frogs are male?
We don't have any information on the distribution of male and female, so we assume they are equally likely. But you're right, if we had information about the sex ratio the answer would change to reflect that.
-
There doesn’t seem to be anything in the question that prevents you from just trying them all, and so automatically getting cured.
p(all three are male) = 1/6.
But I'm sure that's been covered already by the time this post gets read...
-
It simulates the case of seeing which frog croaks.
Huh? How? All I see is that you skip FF and FM as valid trials, leaving only MF and MM so of course it becomes 50% with that flawed logic.
You lick both frogs so it doesn't matter if you know which one croaked. The order doesn't matter but FM and MF are still distinct possibilities (which was what confused me).
-
You saw the left frog croak. Therefore, the left frog is male. The right frog you don't know for sure if it's male or female.
This is different than seeing one frog croak, so you're not sure if the left frog is male and the right frog is female, the right frog is male and the left frog is female, or if they're both male.
You lick both frogs
Like I said, the chance that you're a dumbass who wastes time licking a known male frog.
-
If I have enough time to think about this, I probably have enough time to lick all three frogs.
As soon as you move, you'll startle the frogs. Being ill-equipped to fight you they're likely to flee. By the time you've collected the frog(s) in the direction you initially ran, the other(s) have hopped away, and you didn't see where they went because you had your back to them.
-
Huh? How? All I see is that you skip FF and FM as valid trials, leaving only MF and MM so of course it becomes 50% with that flawed logic.
It's not flawed. It's simulating the case where you saw a particular frog croak. It's probably simpler to simply update the simulation so that you have:
int clear1 = 0;Or you could run it where you set
clear0to0. The results will be the same.You lick both frogs so it doesn't matter if you know which one croaked.
Why would you lick both frogs if you knew for sure that one of them couldn't help you? We're estimating our chances based on what we know. If we have perfect knowledge, then our chance of survival is either 1 or 0. But we have imperfect knowledge, so we're estimating our chances based on what we know.
The order doesn't matter but FM and MF are still distinct possibilities (which was what confused me).
 MF and FM being distinct is what "the order matters" means.
MF and FM being distinct is what "the order matters" means.
-
Also relevant:
-
The problem with this reasoning is that you assume that the possible universes are distributed equally between the four possible frog sets. What if out of 1000 universes, there were 960 such that both frogs are male?
The video establishes the distribution for male and female is 50-50. And I'm not assuming they're equally distributed, I'm asserting they are. Yes, if you experimentally take 1000 samples, it's possible you'll run into a weird situation. We could even calculate the odds of getting 960 MM pairs out of 1000 tries. But I'm not doing that.It's not flawed. It's simulating the case where you saw a particular frog croak. It's probably simpler to simply update the simulation so that you have:
This is what got me mixed up before. Saying "You see one frog croak" is different from saying "You see the left frog croak" or "You see the right frog croak". When you just say "you see one croak", then you are including both scenarios. When you establish "you saw the left frog croak", then you exclude the cases where the right frog croaked and the left one was the female, meaning half of the survival cases, so you're down to 50% odds.
So to get the right odds, you have to be very clear when asking the question as to whether which frog you saw croak matters or not. Saying you saw the right frog croak is irrelevant if you are not excluding from your chances the people who saw the left frog croak.
 Kurt Gödel - Wikipedia
Kurt Gödel - Wikipedia
